Classification

Logistic Regression

It is easy to say that the linear regression predicts a “value” of the targeted variable through a linear combination of the given features, while on the other hand, a Logistic regression predicts “probability value” through a linear combination of the given features plugged inside a logistic function. Linear regression is unbounded, and this brings logistic regression into picture. Their value strictly ranges from 0 to 1.

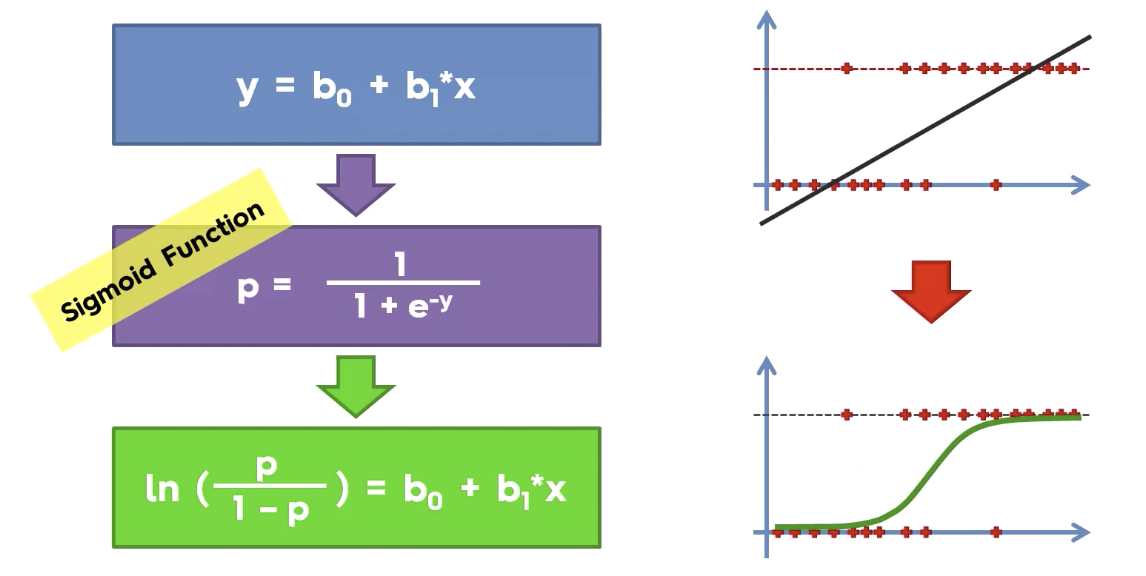
Fig. 13 Logistic regression uses Sigmoid function to transform linear regression into the logit function. Logit is nothing but log of Odds. Then using log of Odds it calculate the required probability.(📖Source)

Cost Function

One more thing to note here is that logistic regression uses maximum likelihood estimation (MLE) instead of least squares method of minimizing the error which is used in linear models. In Linear regression we minimized SSE. In Logistic Regression we maximize log likelihood instead. Linear regression uses mean squared error as its cost function. If this is used for logistic regression, then it will be a non-convex function of parameters (theta). Gradient descent will converge into global minimum only if the function is convex.

Fig. 14 Cost function(📖Source)

Metrics

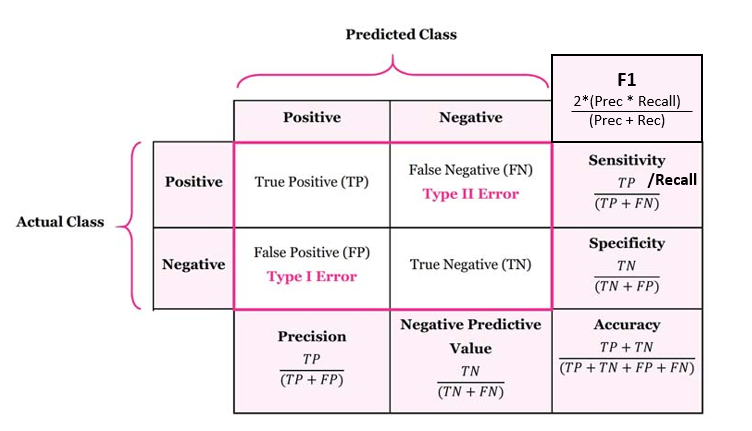
Fig. 15 Confusion Matrix and key Metrics

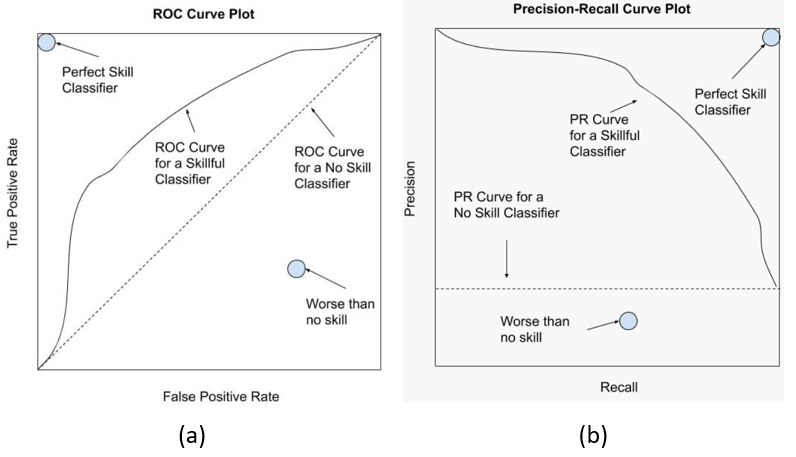
Fig. 16 (a) ROC curve (b) Precision-Recall curve. Both are a helpful diagnostic tool for evaluating a single classifier but challenging for comparing classifiers. Like ROC AUC, we can calculate the area under the curve as a score and use that score to compare classifiers. The focus on the minority class makes the Precision-Recall AUC more useful for imbalanced classification problems. (📖Source)

Questions

Problem: [ROBINHOOD] Interpret Coefficients

How would you interpret coefficients of logistic regression for categorical and boolean variables?

Solution:

Reference: Explanation

Let’s explain this using an example. The table below shows the main outputs from the logistic regression. It is very obvious which are the categorial variables out here:

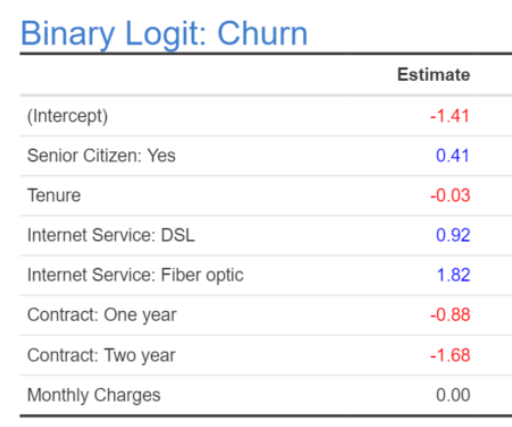
The first category (usually not shown) has a coefficient of \(0\). So, if we can say, for example, that:

• The effect of having a DSL service versus having no DSL service \((0.92 - 0 = 0.92)\) is a little more than twice as big in terms of leading to churn as is the effect of being a senior citizen \((0.41)\).

• The effect of having a Fiber optic service is approximately twice as big as having a DSL service.

• If somebody has a One year contract and a DSL service, these two effects almost completely cancel each other out.

Consider the scenario of a senior citizen with a \(2\) month tenure, with no internet service, a one year contract and a monthly charge of $\(100\). If we compute all the effects and add them up we have:

\(0.41\) (Senior Citizen = Yes) \(- 0.06 (2*-0.03\); tenure) \(+ 0\) (no internet service) \(- 0.88\) (one year contract) \(+ 0 (100*0\); monthly charge) \(= -0.53\).

We then need to add the (Intercept), also sometimes called the constant, which gives us \(-0.53- 1.41 = -1.94\). To make the next bit a little more transparent, I am going to substitute \(-1.94\) with \(x\). The logistic transformation is:

Probability \(= \frac{1} {1 + \exp^{-x}} = \frac{1}{1 + \exp^{1.94}} = 0.13 = 13\%\).

Thus, the senior citizen with a \(2\) month tenure, no internet service, a one year contract, and a monthly charge of $\(100\), is predicted as having a \(13\%\) chance of cancelling their subscription. By contrast if we redo this, just changing one thing, which is substituting the effect for no internet service \((0)\) with that for a fiber optic connection \((1.86)\), we compute that they have a \(48\%\) chance of cancelling.

Problem: Multinomial Logistic Regression

Can Logistic Regression be used for multi class classification?

Solution:

Logistic regression, by default, is limited to two-class classification problems. Some extensions like one-vs-rest can allow logistic regression to be used for multi-class classification problems, although they require that the classification problem first be transformed into multiple binary classification problems.

Multinomial logistic regression algorithm is an extension to the logistic regression model that involves changing the loss function to cross-entropy loss and predict probability distribution to a multinomial probability distribution to natively support multi-class classification problems.

Problem: Choice of Cost Function

In what situations would you recommend using one metric over the another for classification models?

Solution:

It all depends on the use case. For example, a diagnostic lab will be concerned with incorrect positive diagnosis. Hence, they will aim for a high specificity value. On the other hand, for a model predicting loan default rate the goal is to identify even a small chance of default, hence we need the model to maximize sensitivity.